Labels

Selasa, 27 November 2012

Law of Conservation of Momentum

Just like energy, under certain conditions, the momentum of a system will be eternal or unchanging. To provide an understanding of it, it will use the concept of mass center. For example if there is a system consisting of multiple objects with a mass moving with velocity, respectively, then the speed of the center of mass of the system are:
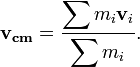
\mathbf{v_{cm}} = { \displaystyle\sum m_i \mathbf{v}_i \over \displaystyle\sum m_i }.
And if the system is moving with accelerated with the acceleration, respectively, then the acceleration of the center of mass of the system are:
\mathbf{a_{cm}} = { \displaystyle\sum m_i \mathbf{a}_i \over \displaystyle\sum m_i }.
Now if the objects are each assigned a style, then these objects each have acceleration:
\mathbf{a_{i}} = { \mathbf{F_i} \over m_i }.
So the acceleration of the center of mass of the system can be expressed as:
\mathbf{a_{cm}} = { \displaystyle\sum \mathbf{F}_i \over \displaystyle\sum m_i }.
Notasi \displaystyle\sum \mathbf{F}_i. a notation stating the resultant force acting on the system. If the resultant force acting on the system is zero (\displaystyle\sum \mathbf{F}_i = 0),then the system is not accelerated (\displaystyle\sum \mathbf{a}_i = 0). If the system is not accelerating, it means the system is the speed of the center of mass of the system is constant (\mathbf{v_{cm}} = constant).So it can be concluded that:
\displaystyle\sum m_i \mathbf{v}_i = constant.
The notation above is a notation of the law of conservation of momentum. So the total momentum of a system is always conserved only if the resultant force acting on the system is zero.
Diposting oleh di Selasa, November 27, 2012
Label:

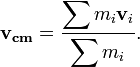
0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)